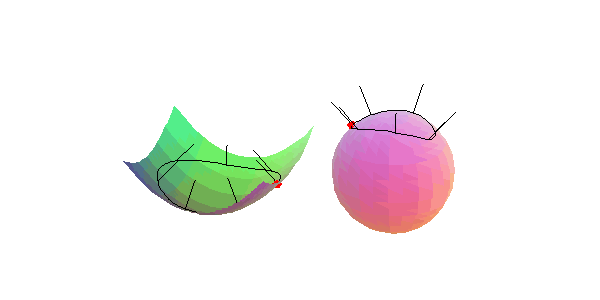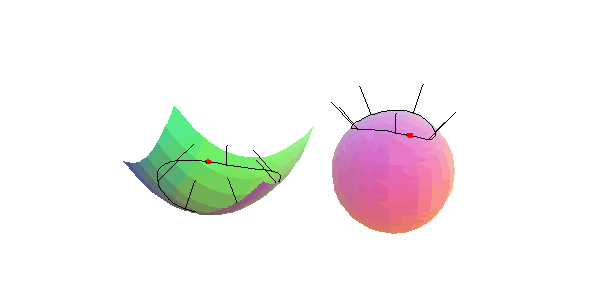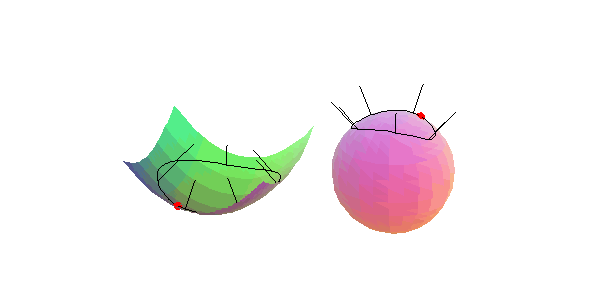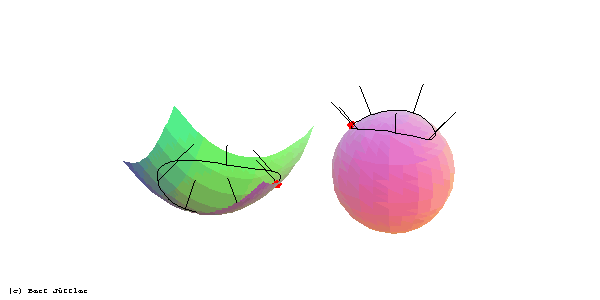
Wir betrachten eine Flächenkurve, die einen gegebenen Punkt einer Fläche im Inneren enthält, und das zugehörige Normalenbild, in der Umgebung eines
elliptischen Flächenpunkts: Der Umlaufsinn der den Punkt einschließenden Flächenkurve und ihres Normalenbildes stimmen überein.
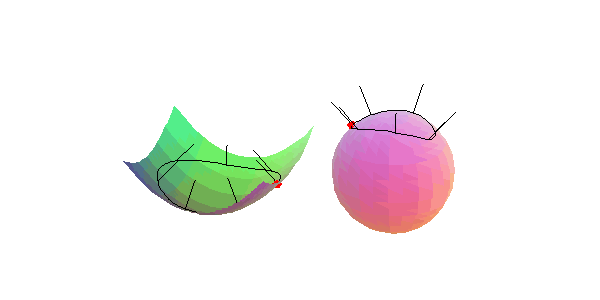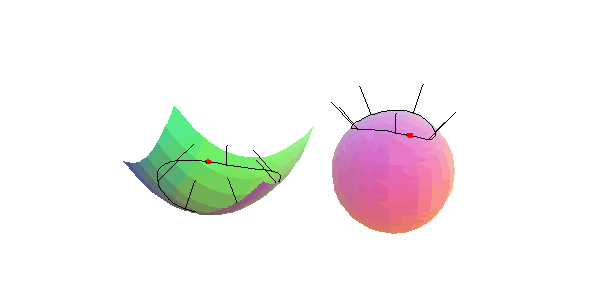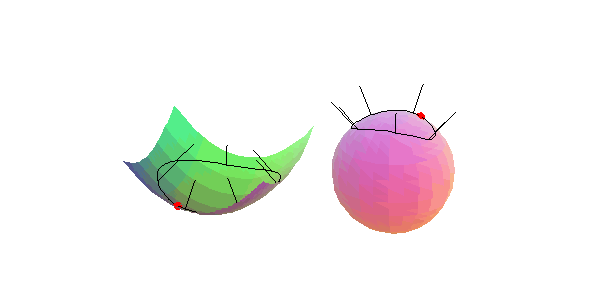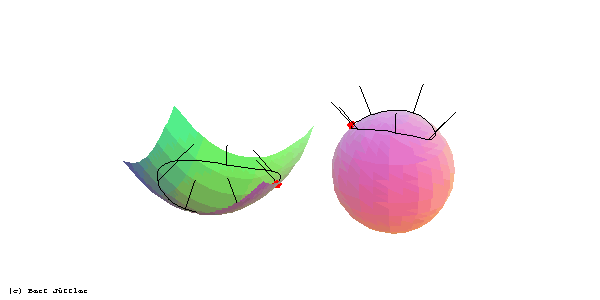
hyperbolischen Flächenpunkts: Der Umlaufsinn der den Punkt einschließenden Flächenkurve ist entgegengesetzt zu dem ihres Normalenbildes.
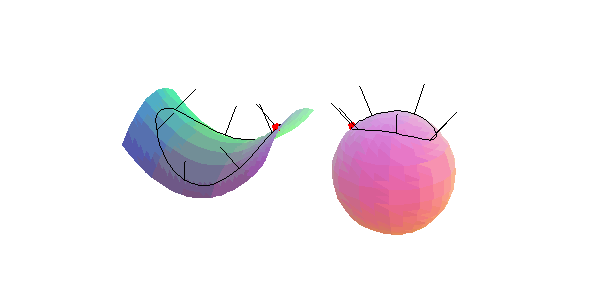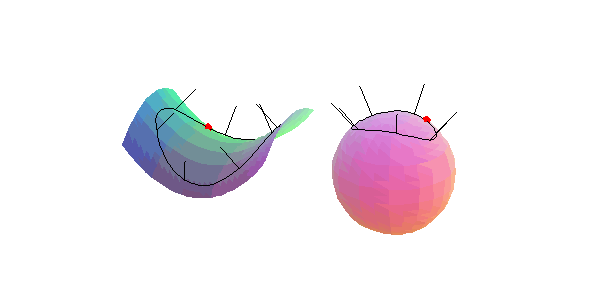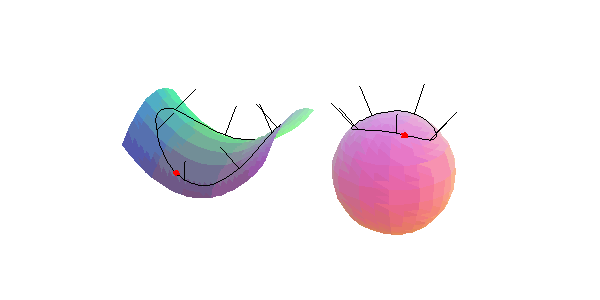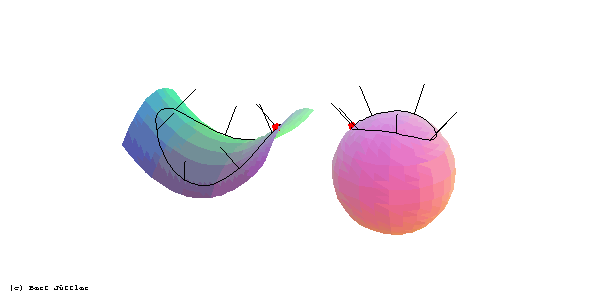
parabolischen Flächenpunkts: Das Normalenbild der den Punkt einschließenden Flächenkurve besitzt einen Doppelpunkt.
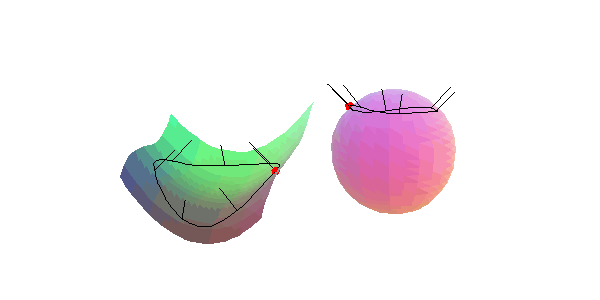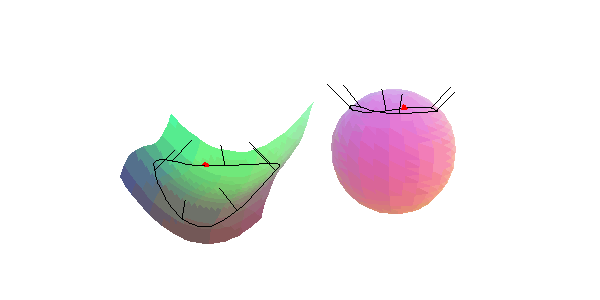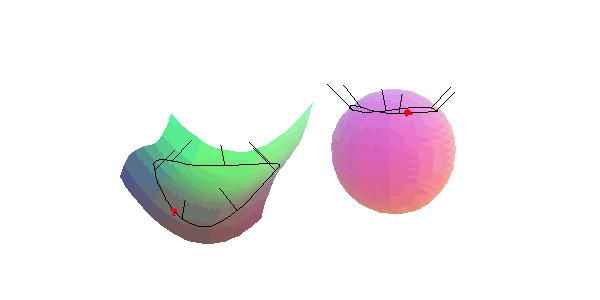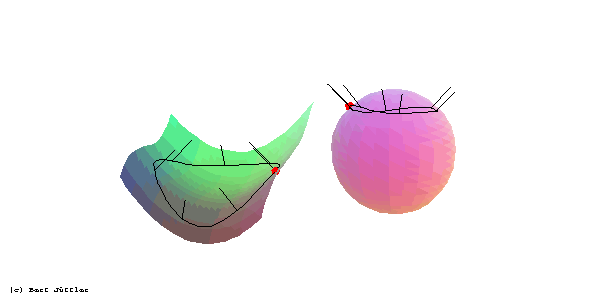
Affensattels: Hier entsprechen einem Umlauf der den Punkt einschließenden Flächenkurve zwei Umläufe des Normalenbildes.
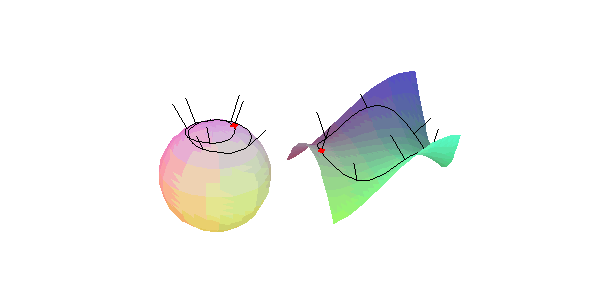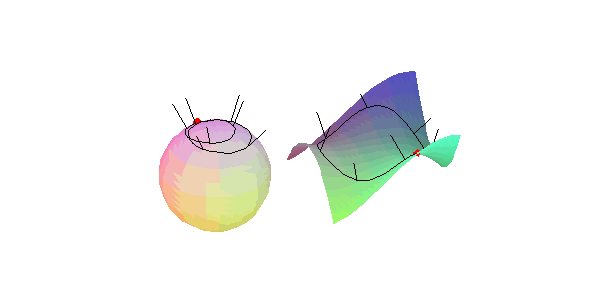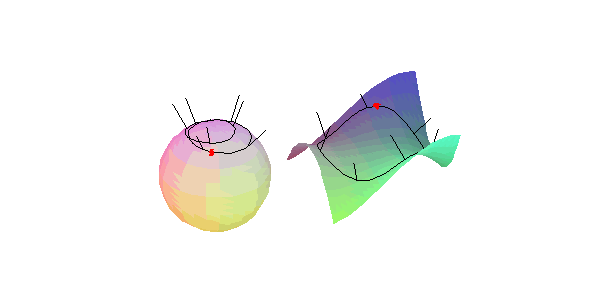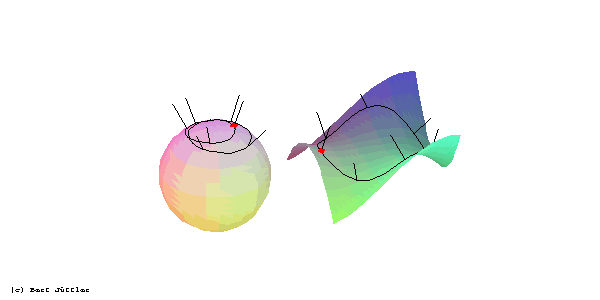
(Literatur: Hilbert/Cohn-Vossen: ``Anschauliche Geometrie'')