Descriptions as booklet in German
Quiz for the Long Night of Science 2024, here

Sample 1: Möbius strip - 3D
Printable pattern page 1
(pdf/
svg),
page 2
(pdf/
svg).
Blue is mountain folding, red is valley folding.
Sample 2: Stanford bunny

A Python script for unfolding triangular meshes in order to create paperfold models at Github
construction manual:
Sheet size 30x30 cm, with numbers:
SVG
Sheet size 30x30 cm, without numbers:
SVG sheet 1,
2,
3,
4,
Sheet size A4, without numbers:
PDF sheet 1,
2,
3,
4,
Stanford bunny made of Lego, see LNDF 2016.


In geometry, Villarceau circles are a pair of circles produced by cutting a torus obliquely through the center at a special angle (from Wikipedia).
Construction period: May 2016 - July 2016, more details here.

A hyperboloid of revolution of one sheet. The strings are straight lines. For any point on the surface, there are two straight lines lying entirely on the surface which pass through the point. This illustrates the doubly ruled nature of this surface. From Wikipedia
Construction period: Feb. 2015 - March 2015, more details here.


In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the Cantor set and Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension, see Wikipedia.
Instructions from the institute for figuring. Card cube instructions.
Construction period: May 2014 - July 2014. No glue was used! More details here.


2017: Grid of Klein bottle made of cable ties
2019: Klein bottle made of plastic
2023: Klein bottle crocheted
Klein's bottle was first described in 1881 by the German mathematician Felix Klein. It is an example of a non-orientable surface. In colloquial terms, it has the property that inside and outside cannot be distinguished, or in other words, that it only has a single side that is both inside and outside at the same time. Therefore, as with the Möbius strip, no continuous normal vector can be defined on the Klein surface. In contrast to the Möbius strip, this surface has no boundary.





2018
The tangent developable of a space curve γ(t) is a developable surface formed by the union of the tangent lines to the curve. From Wikipedia

In geometry, Plücker’s conoid is a ruled surface named after the German mathematician Julius Plücker. From Wikipedia

Weather forecasting is an inaccurate science. Especially the patterns of clouds and their effects are a mystery. One of the first scientists who ventured into the mysteries of weather was the meteorologist Edward Lorenz. In 1963 Lorenz worked on a calculation for weather forecasting, more precisely he developed a simplified mathematical model for atmospheric convection. From these calculations he received the Lorenz Attractor, from which the Lorenz Manifold was developed in 2002. In 2002 the mathematician Hinke Osinga discovered that the computer model of Lorenz Manifold looks like a crochet script. Osinga did not hesitate for long and crocheted the first Lorenz Manifold. The model of the geometricum consists like the original model of 47 rows and 21.989 stitches. In total more than 1 km of yarn was used to crochet the model.



2013, more information of the discoverer of hyperbolic crochet Daina Taimina on the homepage of the Crochet Coral Reef project.
Crocheted hyperbolic models usually consist of double crochets, single crochets, chain stitches and slip stitches. They are crocheted in rounds and every $n$-th stitch will be doubled. The smaller $n$ is, the more crimped the hyperbolic plane becomes.



The Boromean rings are a link of three closed curves, which can not be separated unless one of the rings is removed (property of a Brunnian link).<\p>
A Seifert surface is an oriented surface, which is bounded by a link or knot. In 1961 Martin Gardner presented the Seifert surface of Boromean rings in his column for the first time.

The Hairy ball theorem states that there is no non–vanishing continuous tangent vector field on a 2-sphere. This means that for any continuous function F which assigns each point p on the sphere a vector, such that the vector F(p) is always tangent to the sphere, there is at least one pole where the field vanishes, i.e., there is a point p on the sphere such that F(p) = 0.
The property can also be expressed as ”you can’t comb a hairy ball flat without creating a cowlick” or ”you can’t comb the hair on a coconut”. See Wikipedia

Viviani’s window is a figure eight shaped curve
on the sphere, which is named after the Italian
mathematician and physicist Vincenzo Viviani
(1622-1703) and was described by him
in 1692.
The curve is obtained as the intersection of
the sphere with a circular cylinder of half the
radius, which touches the sphere tangentially
at one point (the double point of the curve).

A hypercube is an n-dimensional analogy to a cube or a square. A 4D-hypercube is also referred to as Tesseract.
In order to recieve a 3D-projection of the Tesseract, one will start with it's 3D-net (shown on the left picture also called Dali cross). By cutting and folding it can be turned into the second figure (right), before reaching the final representation (top). Over all there are 261 possibilities to display the 3D-net of a 4D-Hypercube.
See also Wikipedia.



The model shows an icosahedron which is spanned by three golden rectangles. A rectangle is called golden rectangle if it is composed of a square and a rectangle, such that both rectangles are similar. The aspect ratio of the rectangel is the golden ratio. If we now combine three of these rectangles such that, they have the same center point then we get by connecting neighboring points a Platonic solid with 20 sides.

A Sierpinski Tetrahedron was built of straws during the
long night of science 2014.


In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory. From Wikipedia
Construction plan
An oloid is a three-dimensional curved geometric object that was discovered by Paul Schatz in 1929. It is the convex hull of a skeletal frame made by placing two linked congruent circles in perpendicular planes, so that the center of each circle lies on the other circle. The distance between the circle centers equals the radius of the circles. One third of each circle's perimeter lies inside the convex hull, so the same shape may be also formed as the convex hull of the two remaining circular arcs each spanning an angle of 4π/3. From Wikipedia
Construction period: autumn 2017.

The Gömböc is a body with the special property
of being able to roll back to a certain point,
no matter how it is placed on the ground.
It can be compared to the classic "tumbler toy",
which also gets up again and again from
any position. However, this only manages to
stand up due to heavy weights inside the body.
The two mathematicians Peter Várkonyi und
Gábor Domokos were the first to answer the
question of the existence of such a convex body without hidden weights with yes and to prove it.
See also Gömböc Hompage.

Scutoids are composed of two base planes that have different numbers of edges and at least one further vertex, that is not part of any base plane. Due to that their side surfaces are in general bent. Yet it is especially interesting, that one can construct Scutoids that pack tightly together (meaning that when putting two together the shared side surfaces fit one another perfectly and avoid any space between them). Another special property of Scutoids is, that the neighbouring relationship on the base planes changes due to that extra vertex when going from one plane to the other.


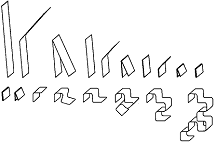
The dragon curve is just like the Koch snowflace a fractal curve which is self similar.
Even the curve uses a finite area its border is infinitely long.
Although the curve looks rather irregular it never crosses itself even once.
Further the dragencurve has a surprisingly simple aspect ration of 3:2.
Also it is an object with which it is possible to tile the plane completely.
An illustrative possibility for finding the n-th iteration of the curve is to fold
a strip of paper in half n times.
If you now open the paperstrip and every side of it is positioned in an angle of 90°
you get the n-th iteration of the dragon curve.

A Hilbert curve (also known as a Hilbert space-filling curve) is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling Peano curves discovered by Giuseppe Peano in 1890. From Wikipedia
A stereographic projection is used for mapping a sphere onto a plane.
More specifically, a perspective projection, so a projection where all lines originate
from one single point, is used. This point is located at the shell of the sphere.
Opposite to it, a tangent plane is used as the projection plane.



The Penrose Tilings are a family of aperiodic
tilings discovered in 1973 by the British mathematician
and physicist Roger Penrose. One of
these tilings is the Penrose P3 tiling, which
consists of a thick and a thin rhombus with
matching rules indicated by circular arcs and
edge modifications.
Online Penrose tiling generator

In geometry, the 120-cell is the convex regular 4-polytope with Schläfli symbol {5,3,3}.
The boundary of the 120-cell is composed of 120 dodecahedral cells with 4 meeting at each vertex. It can be thought of as the 4-dimensional analog of the regular dodecahedron. Just as a dodecahedron can be built up as a model with 12 pentagons, 3 around each vertex, the dodecaplex can be built up from 120 dodecahedra, with 3 around each edge.
From Wikipedia

The 24-cell is a convex regular fourdimensional polytope, which was first described
by the swiss mathematician Ludwig Schläfli in the mid-19th century. It is also
known as icositetrachoron, octaplex, icosatetrahedroid, octacube, hyperdiamond or polyoctahedron,
being constructed of octahedral cells.
Its boundary consists of 24 (regular) octahedron cells, six of which meet at each vertex
and three at each edge. The body contains, in addition to the 24 cells, 96 triangular planes,
96 edges and 24 corners.
The present model was built as part of a seminar at the Institute of Applied Geometry of
metal and fishing line.

A dodecahedron is a 12-sided polyhedron. Dodecahedra come in many different shapes. One of the most familiar shapes of dodecahedra is the regular dodecahedron, which has twelve regular pentagons as faces and is one of the Platonic solids. It has 30 edges, 20 vertices and 160 diagonals. The surface area and the volume of a regular dodecahedron are both related to the golden ratio. The dual polyhedron is the regular icosahedron. With these two polyhedrons there can be constructed many other solids, e.g. the truncated icosahedron (soccer ball), which is the result of taking the intersection of a regular dodecahedron and a regular icosahedron. In total there exists 6 384 634 topologically distinct convex dodecahedra. The number of vertices of these dodecahedra varies from 8 to 20.

Together with the small stellated dodecahedron and the great dodecahedron as well as the great icosahedron the great stellated dodecahedron represents one of four Kepler-Poinsot polyhedra. As a regular geometric object it is bounded by 12 uniform pentagrams which generate 60 isosceles triangles and it is characterized by equality of both any interior and exterior angles with a value of 63,44 °.

In geometry, the truncated icosahedron is an Archimedean solid, one of 13 convex isogonal nonprismatic solids whose faces are two or more types of regular polygons. This geometry is associated with footballs typically patterned with white hexagons and black pentagons. From Wikipedia



The rhombicuboctahedron consists of 18
squares and 8 equilateral triangles. Therefore
it has 48 edges and 24 vertices.
The name originates from the fact that 12 of
the 18 squares are congruent to the rhombi of
the rhombic dodecahedron.


The rhombenicosidodecahedron is one of a total of 13 (without similarity difference, otherwise 15)
Archimedean solids which were probably discovered in the 3rd century BC by the mathematician Archimedes.
The rhombicosidodecahedron gets its name from the congruence of the squares with the rhombuses
of a rhombic triacontahedron. In total, the solid consists of 20 equilateral triangles,
30 squares, 12 regular pentagons and 120 edges, with 10 edges each forming a regular decagon.
With the help of the outer sphere and tangent planes, the deltoid hexacontahedron results as a dual body.

The Pythagoras tree is a recursively created fractal, which was initially described in 1942 by the Dutch maths teacher Albert E. Bosman. The construction is based on the Pythagorean theorem: Starting with a square representing the trunk, two smaller squares are placed on it confining a right angle. This proceeding is recursively applied to the subsequent squares. After some iterations a construct, which resembles a tree, is obtained.

A Möbius strip (also Möbius band or Möbius loop) denotes a surface with only one edge and one side. It can be easily formed by attaching the ends of a paper strip together with a half-twist. Independent of each other this object was first mathematically described in 1858 by Johann Benedict Listing and August Ferdinand Möbius. The Möbius strip is not orientable, this means that it is impossible to distinguish between clockwise and counterclockwise turns with consistency. In detail, an arrow pointing clockwise on the strip would return as an arrow pointing counterclockwise.

2018, The Schwarz lantern is a pathological example of the difficulty of approximating a smooth curved surface with a polyhedron. From Wikipedia


The Soma cube was invented in 1936 by Piet Hein during a lecture on quantum mechanics conducted by Werner Heisenberg.
Its primary function is as an dissection puzzle with the goal of constructing a 3x3x3 cube from seven smaller, individual parts.
There are 240 distinct solutions of the Soma cube puzzle, except for when the cube is rotated or flipped.
Card cube instructions.
including a 12-unit stellated octahedron and a 30-unit stellated icosahedron made of Sonobe modules, a truncated icosahedron, furthermore, a Bascetta-Stern.
No glue was used!


You see four hexagonal tubes which are hollow. The shape of the cavity is a "rhombic dodecahedron", a geometric solid bounded by twelve rhombuses. From George Hart.
Johannes Kepler Universität Linz, Institut für Angewandte Geometrie, Altenberger Str.69, 4040 Linz